High-order Framewise Smoothness-constrained Globally-optimal Tracking
Norimichi Ukita
Asami Okada
Abstract
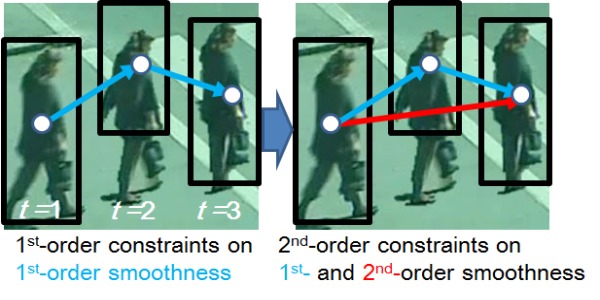
This paper proposes smoothness-constrained globally-optimal tracking of objects. Unlike previous globally-optimal tracking methods, the proposed method can evaluate the smoothness of object trajectories so that the smoothness at a frame can (1) be computed from object detections between the frame and any other frame (e.g., detections even between a long time-interval) and (2) be evaluated simultaneously with multiple neighboring frames. The former and latter properties are called high-order smoothness and high-order constraints, respectively. The high-order smoothness allows us to evaluate the smoothness robustly against noise in detections. The high-order constraints are useful because tracking optimization gets more stable as constraints increase in number. Moreover, smoothness can be evaluated between detections at each frame (i.e., framewise optimization) rather than between short tracks, each of which consists of detections at subsequent frames. Globally-optimal tracking is achieved on a graph where each node corresponds to a detected object region so that detected regions are temporally connected through frames in order to find optimal tracking paths. It is difficult for previous globally-optimal methods to use dynamic features (e.g., velocity), which are required to evaluate smoothness between frames. This is because different tracking paths passing through a node require this node to have inconsistent dynamic features. That is, since the different tracking paths in a graph correspond to spatially-different paths in a scene, each of the different tracking paths has its own dynamic feature at this intersection node. These inconsistent features at the intersection node are prohibited for global optimization on a graph. In the proposed method, such a node is divided such that each divided node has a unique dynamic feature. With public datasets, the proposed method can improve the rate of successful tracking.
Manuscript
Citation
- Norimichi Ukita and Asami Okada,
High-order Framewise Smoothness-constrained Globally-optimal Tracking,
Computer Vision and Image Understanding,
Volume 153C, pp.130-142, 2016.
Doi: 10.1016/j.cviu.2016.05.012
(Impact factor 2016 = 2.498)