In order to realize precision grinding, in-process measurement of grinding wheel wear is required. No method for the in-process measurement of the wear of a grinding wheel with high accuracy in wet condition has been studied because grinding fluid causes a difficulty in measurement. In this paper, a measurement method by hydrodynamic pressure around the grinding wheel caused by grinding fluid is proposed for measuring the wear amount of a grinding wheel. A pressure sensor is set around a grinding wheel. The grinding fluid is supplied to the gap between the grinding wheel and the sensor. Because the viscous fluid is dragged into the clearance between a grinding wheel and a pressure sensor, the hydrodynamic pressure is generated. The relation among hydrodynamic pressure, gap distance and rotational frequency is examined. With the increase in gap distance between the sensor and the disk, the hydrodynamic pressure decreases. By using the measured hydrodynamic pressure, the distance between the sensor in the gap and the grinding wheel can be calculated so that the grinding wheel wear can be measured. The maximum error in using grinding wheels is less than 2 μm in dispersion. By calibrating the relation between hydrodynamic pressure and a gap distance, the measurement can be made towards the actual grinding wheel.
Key words: grinding, wear, hydrodynamic pressure, in-process measurement
1.緒論 2.測定原理 3.基礎実験 4.実際の砥石の測定 5.結論 謝辞 参考文献
各種産業において,製品に要求される機能が高まるにつれて,製品を構成する部品に要求される 加工精度は高くなっている.加工不良を未然に防ぐためには,加工途中における工具の状態を常に認識し, その情報を再び加工工程にフィードバックすれば高精度な加工が持続できると考えられる.
高精度な仕上げ加工には湿式研削加工が適用されることが多い.研削加工の誤差要因の一つに, 工具である砥石の摩耗が挙げられる.そのため研削加工に用いられる砥石の摩耗を測定するために, AEセンサによる接触式検知[1][2],レーザ変位計による方法[3],空気マイクロメータによる方法[4], 超音波による方法[5]等,各種の測定方法がこれまでに研究されている. しかし,湿式研削においては研削液が測定を困難にする要因となっている.そのため,湿式研削における インプロセスの高精度測定は例が少ない.高圧空気で研削液を吹き飛ばす方法[6]やエンドミルの摩耗を対象とし 加工液によるじょう乱を画像処理により補正する方法[7]が提案されているが,研削加工に適用するのに 十分であるとは言えない.
一方,狭い間隔をおいて配置された2物体を相対運動させる場合,そこに粘性流体が存在すれば動圧が 生じることが知られている[8].湿式研削においても,加工時に発生する動圧が被加工物へ与える影響や 研削液の供給量を調べるため,動圧の測定が行われている[9]~[12].
本研究は,湿式研削加工においてインプロセスで砥石の摩耗量を測定することを目的とする. そのために,これまで砥石摩耗量の測定を困難にしていた研削液を積極的に利用し,砥石回りに発生する 動圧を用いて砥石摩耗量を測定する方法を提案する.次に,提案する測定原理を確認するために 円板を用いて行った実験について述べる.最後に,実際の砥石を用いて測定した場合の精度について述べる.
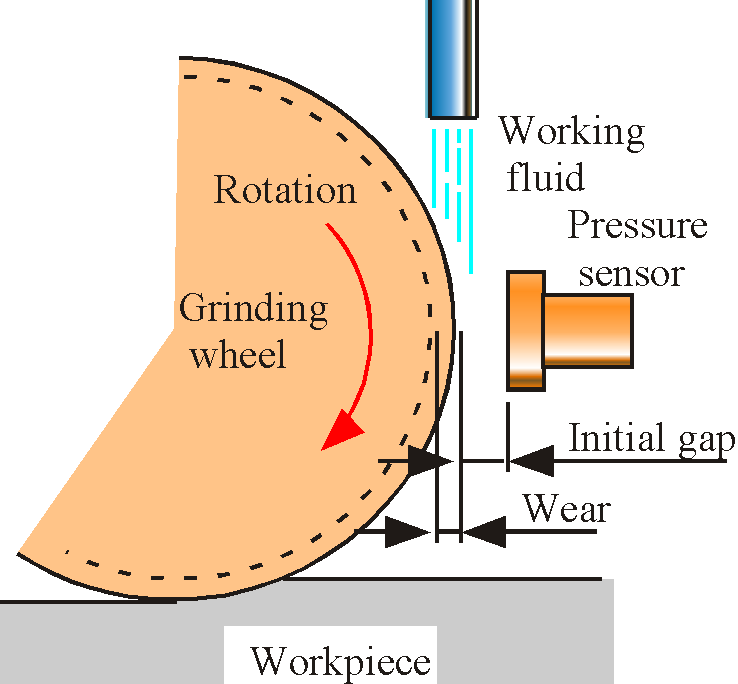
提案する手法を平面研削に適用する場合の測定原理を図1に示す. 砥石作業面近傍に圧力センサを設置する.そして砥石作業面とセンサ間に研削液を供給する. 砥石の回転によって研削液が砥石と圧力センサ間のギャップに引き込まれ動圧が発生する. この動圧を圧力センサで測定する.このとき,ギャップと動圧の関係が明らかであれば, ギャップの変化すなわち砥石の摩耗を測定できる.本手法は,砥石,被加工物および研削液の 電気磁気的な特性の影響を受けない.また,研削液を積極的に利用するため,光学的手法の ような光のじょう乱の問題がない.したがって,従来の非接触センサを用いた方法に比べ容易に かつ高精度に測定することが可能となると考えられる.また,加工に用いる研削液を そのまま利用することが可能であるため,付加する装置が少なくてすむという利点を持つ.
 |
| Fig. 1 Principle of measurement by uging hydrodynamic pressure |
図1を解析する場合のモデルを図2に示す.砥石の半径がR,周速がU,ギャップの最小値がh0である. また,砥石の幅は2b,粘性流体が存在する長さは2Lである.粘性流体の密度, 粘性は一定であると仮定する.
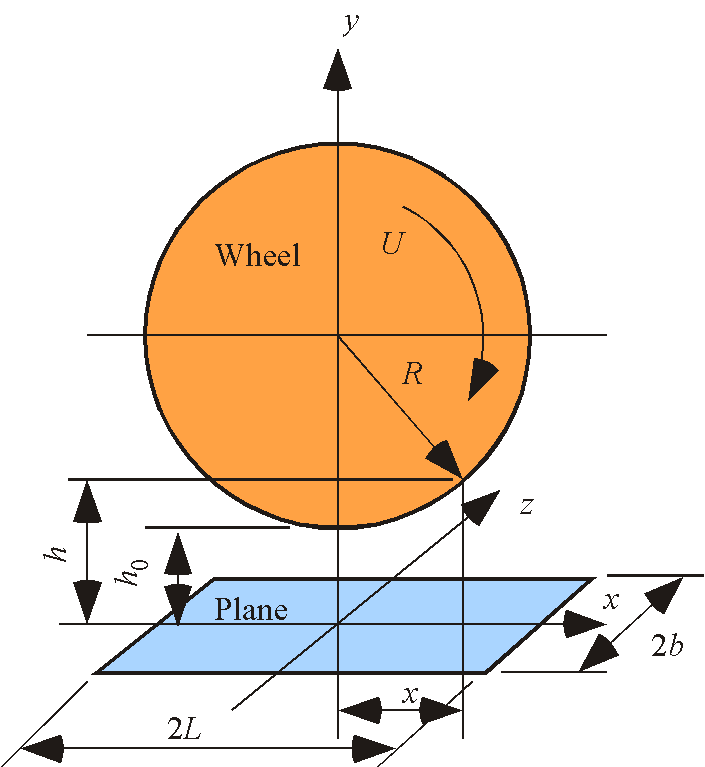 |
| Fig. 2 Analysis model of hydrodynamic pressure |
加工中にインプロセスで測定する場合は,最初はギャップが短いが加工が進むにつれて ギャップは比較的長くなる.そのため,加工の初期はレイノルズ数[13]が1より小さいことが 多く研削液に働く慣性力を無視できるが,途中から考慮しなければならない領域になる. また,研削液の存在するの範囲が広い場合にも端の方ではギャップが大きくなるため慣性力が 無視できない.そのため,全領域を通して解析する場合にはナヴィエ・ストークスの式[14]を 解く必要がある.
ここで,センサを変位させることによるギャップの変化と円板の半径の変化によるギャップの 変化とが圧力に与える影響の違いを考える.まず,センサを変位させる場合にはdR=0であり, h0の変化がギャップの変化量となる.この場合には,研削液に働く慣性力とギャップ長に影響を 与える.これらは,ナヴィエ・ストークスの式のパラメータおよびそれを用いて解析する際の 境界条件として用いられる量である.次に,砥石が摩耗する場合には-dR=dh0であり, 砥石半径の変化がギャップの変化量となる.そして,上記の2つの量ののほかに砥石の周速にも 変化を与える.しかし一般にR>>dRであるため,砥石の摩耗による周速の変化は無視できる. したがって,砥石と平板の間隔を変化させても,砥石径を変化させても動圧の変化はほぼ同じ 結果となると考えられる.したがって3章以下では,主に前者により提案する手法の特性を評価する.
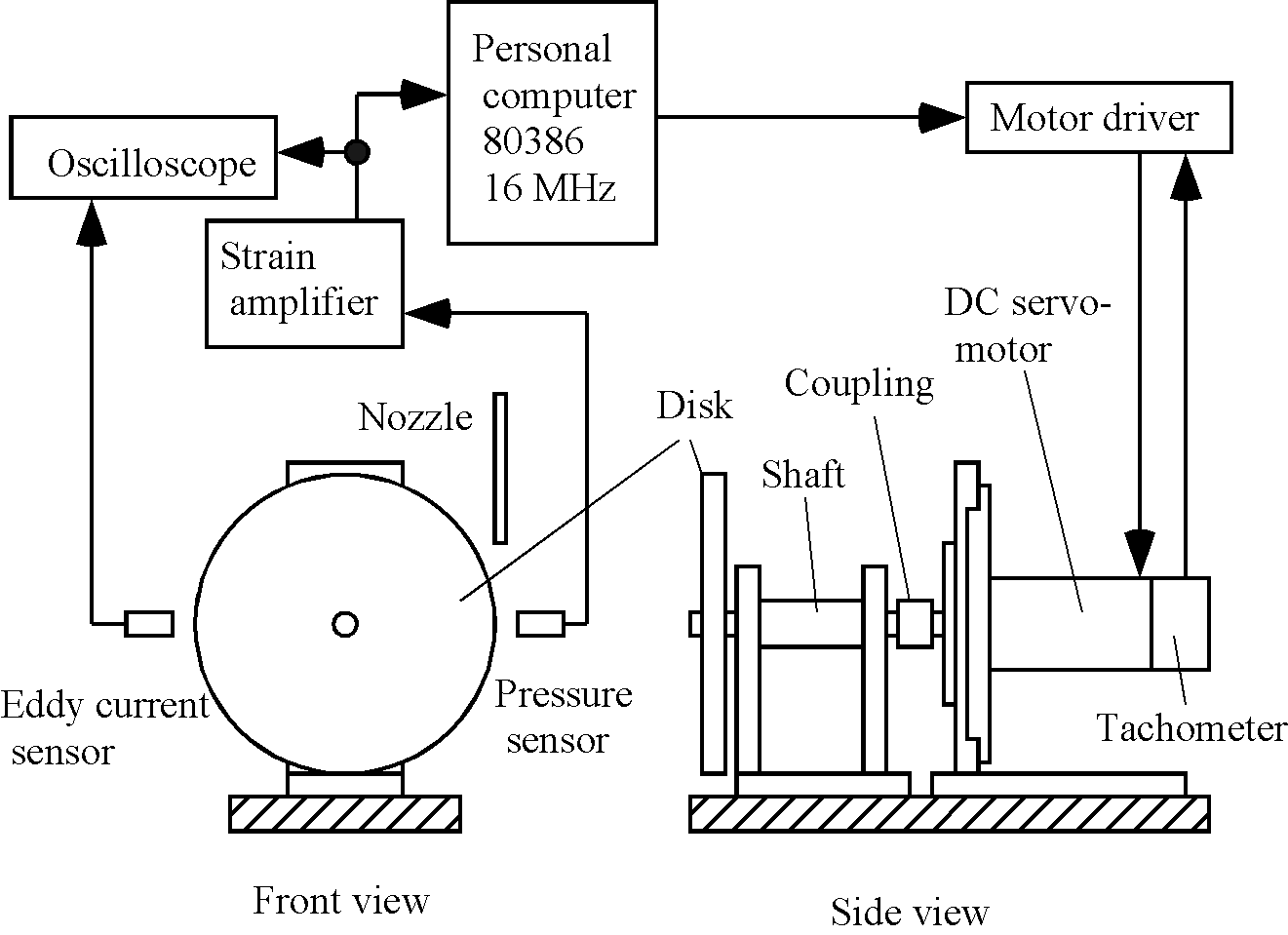
測定原理を確かめるために製作した装置の構成を図3に示す.この装置ではモータで研削砥石の 代わりに円板を回転させ,その円板の円周部(砥石では作業面に当たる)と圧力センサ間に水を 供給することで発生する動圧を測定する.円板はアルミニウム製で,直径は200mm,厚さは10mmである. この円板はワイヤ放電加工により製作した.軸の振れを防ぐため,両端をボールベアリングで支持した. 円板を回転させるためにタコジェネレータ付きDCサーボモータを使用した.モータを回転させる 電源には市販のドライバを使用した.水の供給量は4l/minとした.
 |
 |
| (a) Setup | (b) Appearance |
Fig. 3 Experimental setup for trial measurement |
|
動圧の測定にはダイヤフラム型圧力センサを用いた.直径が6mm,定格容量が0.098Paで,固有振動数は 22kHzである.圧力センサの出力は動ひずみアンプ(周波数範囲:DC~200kHz)を使用して増幅した. 図4に圧力センサの取付方法を示す.圧力センサが円板円周部に直接接触することを防ぐために, SUS304の平板に埋め込んだ.さらにこの平板をxyzステージに取り付けることにより,センサの位置を 自由に設定できるようにした.
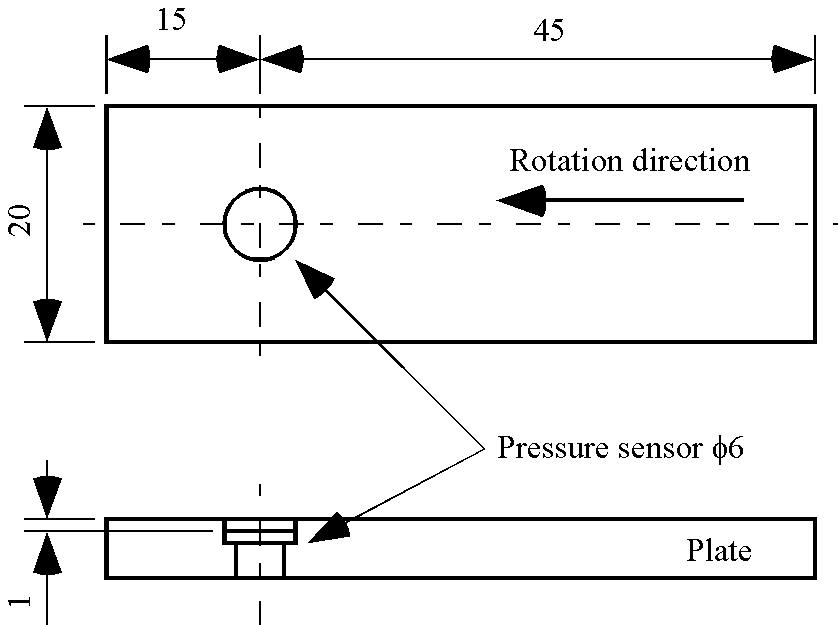 |
Fig. 4 Arrangement of pressure sensor |
圧力センサの出力とギャップを比較するために渦電流式変位センサ(感度:0.2mm/V,分解能:0.4μm, 応答周波数:18kHz,プローブ直径:5mm)でギャップの相対変化を測定した.このセンサは円板の 回転軸に対し圧力センサと対称の位置に取り付け,圧力センサと同時に測定した.
圧力センサからの出力の平均値を求めるためと回転数の指令値を与えるためにパーソナルコンピュータ (80386,16MHz)を使用した.
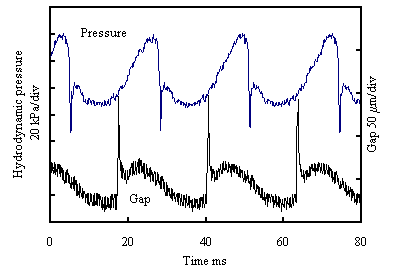
製作した基礎実験用回転装置を使用して,発生する動圧の大きさを調べた.回転数が2000min-1, 最小ギャップが1μmの場合の圧力センサおよび渦電流式変位センサの出力例を図5(a)に示す.動ひずみ 測定器を用いた場合,圧力センサの感度は1.02×10-4V/Paとなった.圧力センサと渦電流式変位センサは 回転軸に対して対称に配置されている.圧力センサの波形を半周期ずらし,さらに出力を反転した波形を 渦電流式変位センサの出力と比較した結果,両者が一致することを確認した.突起状の波形は, ワイヤ放電加工により円板を製作する際にできた幅約200μmの溝が原因である.また,この渦電流式 変位センサの波形から考えると,本装置の円板は取付け時に20μm偏心している.この偏心も圧力変化として 出力されていることがわかる.
 |
 |
(a) Time domain |
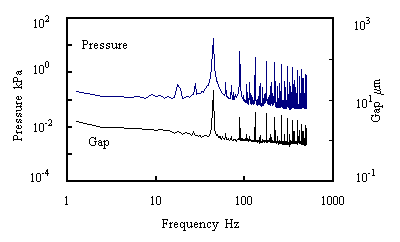
(b) Frequency domain |
Fig. 5 Example of outputs of sensors |
|
それぞれのセンサからの出力を周波数解析した結果を同図(b)に示す.最も高いピーク値である46Hzの 部分は円板の回転数2800min-1に相当する部分である.この図からも圧力センサと渦電流式変位センサの データがほぼ一致していると言える.
円板の回転数とギャップを変化させた場合の動圧の平均値を図6に示す.回転数は1000min-1から 2800min-1まで200min-1間隔で変化させた.最小ギャップは1μmから10μmまで変化させた. 縦軸の圧力は,大気圧を差し引いた値である.どのギャップにおいても回転数の増加に対し動圧も 単調増加することが明らかになった.また,回転数が大きいほどギャップ変化時のセンサ出力の 変化は大きかった.
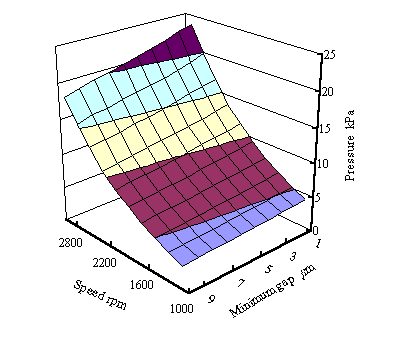 |
| Fig. 6 Relationship among pressure, speed and gap length |
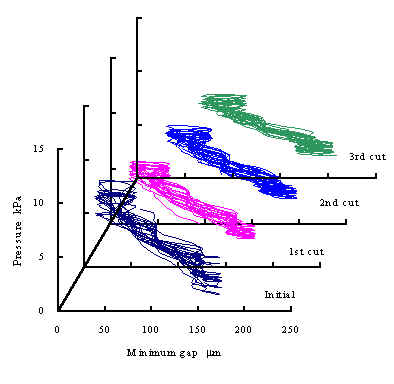
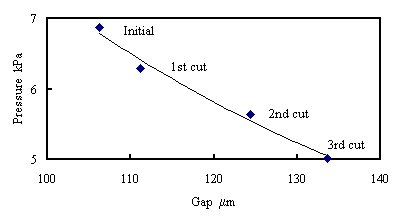
前節の実験では円板を摩耗させる代わりにステージを移動させることでギャップを変化させていた. 本節では円板を細目平形鉄工やすりを軽く押し当てて摩耗させることによりギャップを変化させた. 測定に使用した円板回転数は2800min-1で,周速は29.3m/sである.初期状態における最小ギャップは 40μmに設定した.図7(a)にギャップと圧力センサ出力のリサージュ図を示す.位相を調整して得られた 渦電流式変位センサによる測定値を真のギャップとして横軸に示し,縦軸に圧力センサの出力を示した.
最初に摩耗なしの状態で測定し,その後3回に分けて行った摩耗によるギャップの増加に対して動圧は 単調減少した.摩耗後は,初期状態の分布上を摩耗量分移動させた分布が観察された. 同一ギャップにおいて圧力にばらつきがあるのは,水流の乱れ,回転軸の剛性不足による振動やセンサ からの電気的なノイズであると考えられる.しかし,これらの外乱はランダムなノイズであることが多いため, 平均化することで半径の減少を測定することができる.同図(b)に同図(a)の平均値を示す.点は各測定値の 平均値であり,実線は摩耗させる前のリサージュ図形から求めた回帰曲線である.それぞれの平均値が 回帰曲線とほぼ一致していることがわかる.
 |
 |
| (a) Trajectory of pressure to gap length | (b) Average pressure and gap length |
| Fig. 7 Influence of wear of wheel on pressure | |
実際の研削砥石への適用可能性を調べた.平面研削盤 (砥石回転数1800min-1)の主軸に砥石を取り付けた. 使用した研削盤では砥石側方に圧力センサを取り付けることができなかったため,xyzステージを用いて 研削盤のテーブル上に圧力センサを設置した.研削砥石作業面と圧力センサ間には水溶性研削液を25l/minで 供給した.座標系を図8に示す.砥石中心から垂線を下ろしセンサを取り付けた平板上面と交わる点を原点とし, 研削盤の正面から見て右向きを+x,上向きを+y,手前向きを+zとする右手座標系とした.研削液は+x側から 原点に向けて供給した.
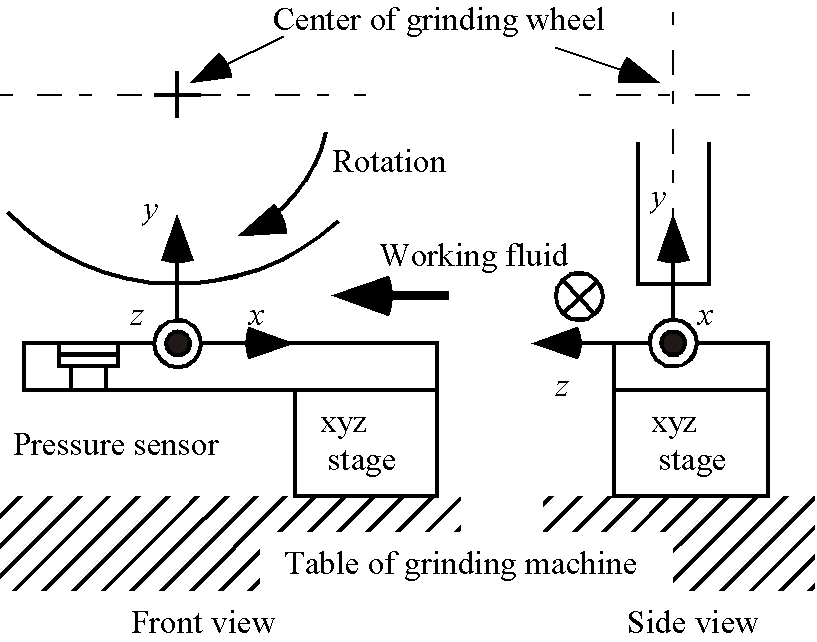 |
Fig. 8 Coordinate system of grinding machine |
今回の実験ではD#400,WA#46,WA#800の3種類の砥石を使用した.表1にこれらの砥石の仕様をJIS-R6210の 形式で示す.砥石の外形の違いが動圧に影響を及ぼすことのないよう外径はすべて305mmとした.
Table 1 Specifications of grinding wheels |
|||
| D#400 | WA#46 | WA#800 | |
Outer diameter mm |
305 |
305 |
305 |
Inner diameter mm |
127 |
127 |
76.2 |
Width mm |
10 |
38 |
32 |
Grain |
Diamond |
White fused alumina |
White fused alumina |
Mesh size |
400 |
46 |
800 |
Grade of hardness |
H |
H |
I |
Structure |
6 |
7 |
2 |
Bond |
B |
V03 |
E |
まず,動圧が最大となる点を調べるためにx方向に圧力センサを0.5mmずつ移動させ,x方向の動圧の分布を 測定した.図9に実験で得られた圧力分布を示す.WA#800の砥石を使用し,最小ギャップが0μm,10μm, 20μmの3種類の場合について測定した.x=+1.5mmで動圧が最大になった.以下の実験ではこの最大点が現れる 位置において動圧の測定を行った.
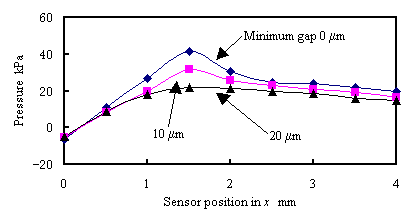 |
| Fig. 9 Measured pressure distribution in x direction |
次に,砥石はWA#800を使用しz方向(砥石軸方向)の圧力分布を測定した.圧力センサのx方向位置は+1.5mmとし, z=0~20mmの範囲で1mmごとに測定した.圧力センサと砥石作業面のギャップは0μmに設定した. 図10に測定結果を示す.センサ受圧面の円周部が砥石作業面の端に近づくにつれ,動圧は徐々に減少した. また,圧力センサの受圧面の円周部が砥石作業面の端と一致する位置でも動圧が確認された. 圧力センサの受圧面の円周部が砥石作業面の端から出た位置では動圧が確認されなかった.したがって, 砥石角部の摩耗量の測定はこのままでは不可能である.角部近傍まで測定するには圧力センサの受圧面を 小さくする必要があると考えられる.
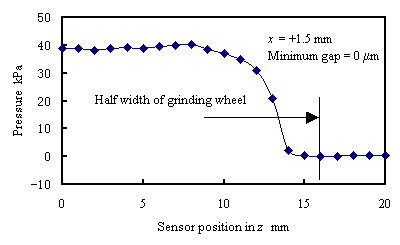 |
| Fig. 10 Measured pressure distribution in z direction |
次に,粒度の影響を検討した.図11に最小ギャップと動圧の平均値の関係を示す.最小ギャップを0μmから 100μmまで10μmずつ変化させて,そのときの動圧を圧力センサで測定した.周速は28.7m/sとした. すべての砥石においてギャップの増加に伴い圧力センサ出力は単調減少した.
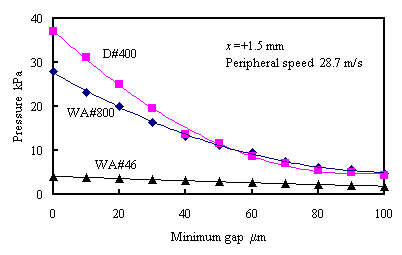 |
Fig. 11 Influence of mesh size |
粒径の小さいD#400と粒径の大きいWA#46を比較すると,WA#46はD#400に対し出力がかなり小さかった. 粒径が大きいため,平均ギャップが広がることが原因であると考えられる.D#400とWA#800を比較すると, 粒径の小さいWA#800の方が小さく出力される.これは前に述べた粒径が大きい砥石の方が動圧は小さくなる ということに反する.WA#800では目詰まりを防ぐために気孔が含まれているボンドを使用している. その気孔の影響で設定したギャップよりも平均ギャップが増加し,発生する動圧が小さくなったと考えられる.
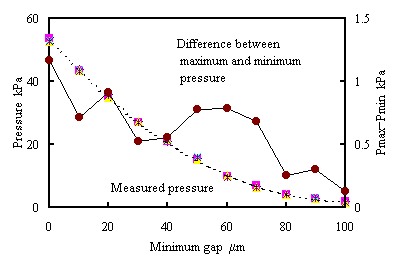
仕上げ加工に用いられる粒度の大きい砥石を使用し,測定された圧力のばらつきを検討した.それぞれの 砥石において,最小ギャップを0μmから100μmまで10μmずつ変化させ,そのときの圧力センサの平均出力を 5回ずつ測定した.図12(a)にD#400を使用して得られた結果を示す.D#400を使用した測定では,測定値の 最大値と最小値の差は0μmのときに最大であり,1.17kPaとなった.これは0?mにおける平均値の2.2%であった. 同図(a)から最小ギャップが0μmの付近では感度が0.96kPa/?mとなるので,この値を用いて上記の差を変位に 換算すると1.2μmとなる.またWA#800を使用して得られた結果を同図(b)に示す.測定値の平均値と最も差が 大きい測定値との差は最小ギャップが20μmのときに最大であり,0.38kPaであった.これは20μmにおける 平均値の1.6%であった.同図(b)から最小ギャップが20μmの付近では感度が0.32kPa/μmとなるので, この値を用いて上記の差を変位に換算すると1.2μmである.このように,最小ギャップが小さい場合には 圧力の測定値のばらつきが大きいが,測定値の平均も大きいため変位換算ではばらつきが小さくなる. しかし,最小ギャップが小さい場合には,測定値の平均が小さくなるため変位換算ではばらつきが大きくなる. したがって,本手法で高精度に測定するためには,最小ギャップを数十μm程度以下とすることが望ましいと 考えられる.
 |
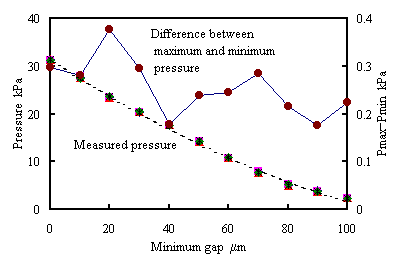 |
| (a) D#400 | (b) WA#800 |
| Fig. 12 Dispersion of measured pressure | |
研削液の温度が安定するまでは圧力センサの出力が変動する傾向が見られた.これは,圧力センサの 温度特性が原因であると考えられる.
本論文の内容をまとめると以下のようになる.
(1)本研究では,湿式研削における砥石摩耗量のインプロセス測定を目的とし,動圧を利用した測定法を 提案した.本手法では測定のための媒体として研削液を利用するため,付加する装置が少なくてすむと いう利点を持つ.
(2)3種類の砥石を使用し,提案した方法でギャップと動圧の変化を測定した. その結果,動圧の大きさは砥石の粒度や気孔の影響を受けることが明らかになった. しかし,いずれの場合でもギャップの増加に対し動圧は単調減少した.
(3)同一ギャップ長における圧力のばらつきはギャップが小さい範囲では2%程度であった. 以上のことから,ギャップと動圧の関係を校正することで本手法を砥石の摩耗量測定に適用することが 可能であると考えられる.
今回は使用した研削盤の制約により,実際の加工における砥石の摩耗に関してはインプロセスで測定する ことができなかった.今後は,圧力センサの出力波形を周波数領域において詳細に解析することにより, 目づまり,目つぶれ,ドレッシングの影響等についても検討を行う予定である.
実験の遂行に当たり静岡理工科大学・大塚二郎教授,越水重臣助手から有益な御助言をいただきました. 実験にあたり豊田工業大学・太田勝助手,同試作工場の皆様にご協力いただきました. 本研究の一部には高度自動化技術振興財団,スズキ財団の研究助成を用いました. 記して感謝いたします.
[1] W. P. Dong, L. Annecchino and J. A. Webster: On-Line Measurement of Grinding Wheel Wear Using Acoustic Emission, Proc. 11th Annual Meeting of Am. Soc. Prec. Eng., Monterey, California, USA, (1996) 566.
[2] J. Webster, W. P. Dong and R. Lindsay: Raw Acoustic Emission Signal Analysis of Grinding Process, Ann. CIRP, 45, 1, (1996) 291.
[3] 大和田優,鶴岡光義,宮原克敏,太田稔:加工現象計測システムの開発,砥粒加工学会誌,39,1 (1995) 46.
[4] H. J. Schreitmuller and M. Dederichs: Peneumatisches Mesverfahren zur Ermittlung des Schleifscheibven-verschlieses, Ind. Anz., 93, 68 (1971) 1733.
[5] G. Spur and F. Leonards: Sensoren zur Erfassung von Prozess-kenngrossen bei der Drehbearbeitung, Ann. CIRP, 24, 1, (1975) 349.
[6] 坂本治久,赤見知洋,清水伸二:研削作業面トポグラフィのインプロセス測定の試み,1999年度精密工学会春季大会学術講演会講演論文集,(1999) 648.
[7] 笠島永吉,Oleg Ryabov,森?和男:レーザセンサを用いたインプロセス工具モニタリング法,日本機械学会論文集C編,63,308 (1997) 199.
[8] たとえば,木村好次,岡部平八郎:トライボロジー概論,養賢堂,(1982) 89.
[9] 植松哲太郎,張波,蒔崎剛,鈴木清:研削加工液の動圧挙動の測定,砥粒加工学会誌,41,11 (1997) 438.
[10] 宮地隆太郎,林孝:潤滑機構の観点から見た平面研削加工面の圧力分布の実験的検討,1997年度精密工学会秋季大会学術講演会講演論文集,(1997) 399.
[11] 横川和彦,谷内聖,田辺実,向井良平,伊東暁,大坪晴夫:研削油剤供給法とその研削性能におよぼす影響(第2報),昭和55年度精機学会春季大会学術講演会講演論文集,(1980) 428.
[12] M. Yokogawa and K. Yokogawa: Improving Grinding Performance of CBN Wheels by Dual-fluid Supply Method, Int. J. Jpn. Soc. Prec. Eng., 27, 1 (1993) 11.
[13] たとえば,生井武文,井上雅弘:粘性流体の力学,理工学社,(1978) 61.
[14] たとえば,中林功一,伊藤基之,鬼頭修己:流体力学の基礎(1),コロナ社,(1993) 116.
Last modified on 01/23/2002 at 17:04:14 by Katsushi Furutani